光明实验室基础智能研究团队携手深圳大学最新成果：OptEx: Expediting First-Order Optimization with Approximately Parallelized Iteration。作者：Yao Shu, Jiongfeng Fang, Ying Tiffany He, Fei Richard Yu。该论文已被神经信息处理系统大会（简称NeurIPS）2024所接受。

论文：

https://openreview.net/pdf?id=MzNjnbgcPN

代码：

https://github.com/youyve/OptEx

该项目主要基于JAX和PyTorch开发，不仅支持英伟达GPUs、苹果MPS和CPUs，还兼容国产算力平台昇腾NPUs，为国产算力生态提供了新的算子。

摘要

一阶优化（FOO）算法在诸如机器学习和信号去噪等众多计算领域中具有关键作用。然而，当应用于复杂任务（如神经网络训练）时，由于需要大量的顺序迭代才能收敛，往往会导致显著的效率低下。为此，我们提出了通过近似并行迭代加速的一阶优化框架（OptEx），这是第一个通过利用并行计算来缓解迭代瓶颈、提升FOO效率的框架。OptEx使用核化梯度估计，利用历史梯度进行未来梯度的预测，从而实现迭代的并行化——这一策略曾被认为是不切实际的，因为FOO算法固有的迭代依赖性。我们为核化梯度估计的可靠性以及基于SGD的OptEx的迭代复杂性提供了理论保证，证实随着历史梯度的累积，估计误差趋于零，并且基于SGD的OptEx在并行度为N的情况下，相较于标准SGD具有θ(√N)的有效加速率。我们还通过大量的实证研究，包括合成函数、强化学习任务以及在不同数据集上进行的神经网络训练，充分展示了OptEx带来的显著效率提升。

概览

一阶优化（FOO）算法，如随机梯度下降（SGD）、Nesterov加速梯度（NGA）、AdaGrad和 Adam 等，已经成为众多计算领域的基石，推动了从强化学习到机器学习等领域的进步。这些算法以其基于梯度更新的简单迭代形式而闻名，是解决简单和复杂优化问题的基础。然而，当应对复杂函数时，这些算法通常会遇到显著的优化效率问题，特别是在实际中评估函数值和梯度的计算代价高昂且需要大量顺序迭代才能收敛的情况下，例如深度强化学习和神经网络训练。

为此，已有大量文献通过并行计算显著提升FOO的优化（如时间）效率，主要通过减少每次迭代中函数和梯度的评估时间。例如，在神经网络训练的特定领域中，基于并行计算的技术，如数据并行、模型并行和流水线并行，已经被应用于通过同时处理多个输入样本和网络组件来减少损失函数和参数梯度的评估时间。然而，据我们所知，利用并行计算减少收敛所需的顺序迭代次数，以此缓解FOO中的优化效率问题，尚未得到广泛研究。与仅减少每次迭代评估时间的方法不同，后者往往需要在特定领域（如神经网络训练）中投入大量人力，而减少顺序迭代次数更具通用性，因为它不需要这些特定领域的额外努力，因此在实践中具有更广泛的应用潜力。这突显了探索在标准FOO中并行化顺序迭代的潜力。

然而，FOO中的固有迭代依赖性——每次迭代的输出作为下一次迭代的输入——对独立和并行的迭代执行构成了重大障碍，因此在标准FOO中实现迭代并行化几乎是不可能的。为了解决这一问题，我们开发了一个全新的框架，称为基于近似并行迭代加速的一阶优化（OptEx），该框架能够克服标准FOO中的固有迭代依赖性，从而使FOO中的迭代并行化成为可能。具体来说，我们的框架首先提出了一种新颖的核化梯度估计策略，利用优化过程中历史梯度来预测域内任意输入的梯度，使这些估计梯度能够在标准FOO算法中用于确定未来几次迭代的输入。我们进一步引入了可分离核函数和局部历史梯度的技术，以提高这种梯度估计的计算效率。然后，我们将标准FOO算法与这种核化梯度估计相结合，以有效地确定接下来的N次顺序迭代的输入（即代理更新），旨在近似真实的顺序更新，并绕过标准FOO中的迭代依赖性。最后，我们通过利用并行度为N的并行计算，基于代理更新获得的这些$N$个输入，使用真实梯度并行执行标准FOO算法，完成了标准FOO的近似并行迭代。

除了提出创新的OptEx框架外，我们还建立了严格的理论保证和广泛的实证研究来支持其有效性。具体来说，我们为核化梯度估计的估计误差提供了理论界限。值得注意的是，随着历史梯度数量的增加，该误差在广泛的核函数中渐近为零。这表明我们的核化梯度估计可以有效地进行代理更新，帮助并行化FOO中的顺序迭代。

在此基础上，我们给出了基于SGD的OptEx的顺序迭代复杂性的上下界，表明基于SGD的OptEx能够以θ(√N)的加速率减少标准FOO算法的顺序迭代复杂性，其中N为并行度。最后，通过包括合成函数优化、强化学习任务以及在图像和文本数据集上的神经网络训练在内的大量实证研究，我们展示了OptEx在加速现有FOO算法方面的一致优势。

总结起来，本工作的贡献包括：

✦ 据我们所知，我们是第一个开发出能够利用并行计算近似并行化FOO中的顺序迭代的通用框架（即OptEx），从而显著减少FOO算法的顺序迭代复杂性。

✦ 我们首次给出了基于SGD的OptEx的迭代复杂性的上下界，该方法在并行度为N的情况下具有的有效加速率。

✦ 我们进行了广泛的实证研究，包括θ(√N)合成函数优化、强化学习任务以及在图像和文本数据集上的神经网络训练，以支持OptEx框架的有效性。

结果

图2显示了OptEx在不同维度的合成测试函数（如Ackley、Sphere、Rosenbrock等）上相较于其他算法（Vanilla和Target）需要更少的顺序迭代（T）来达到相同的optimality gap。这表明OptEx通过其并行化近似迭代的机制在高维优化问题上能够更快收敛。尤其是对于高维度的场景（如d=10^5），OptEx的性能优势更加明显，说明该方法在复杂、高维空间下具有良好的扩展性。

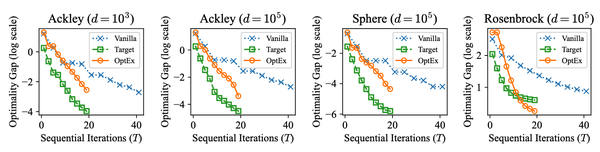
图3表明，OptEx在多个RL任务中（如Cartpole, Acrobot, Lunar Lander, Mountain Car）均能快速提高累积平均奖励。与其他方法相比，OptEx能在更少的顺序迭代次数内获得更好的策略更新效果。尤其是在具有较大状态空间（如Acrobot和Lunar Lander）和较复杂的策略学习任务（如Mountain Car）中，OptEx在减少负奖励和提高正奖励方面具有显著优势。

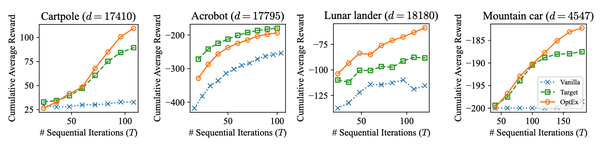
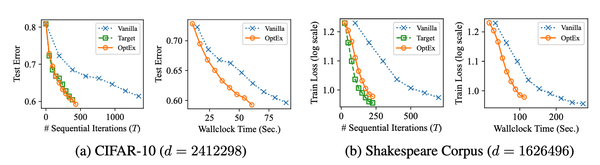
图4表明对于CIFAR-10 (d = 2,412,298) 和 Shakespeare Corpus (d = 1,626,496) 这两个高维任务，OptEx明显减少了顺序迭代次数 (T) 和运行时间 (Wallclock Time) 来达到相同的优化效果。在测试误差和训练损失的下降趋势中，OptEx 相较于 Vanilla 和 Target 具有更快的下降速度，表明其在减少测试误差和训练损失方面能够更有效地提升优化效率。图中显示，OptEx 不仅在顺序迭代次数上更快收敛，还在真实时间（Wallclock Time）维度上大幅减少了优化所需的时间。特别是在 CIFAR-10 和 Shakespeare Corpus 的实验中，OptEx 在相同时间内达到了显著更低的误差和损失。这表明 OptEx 在实际应用中的加速效果尤为显著，能够节省大量的计算资源和时间。从两个任务的高维度 (CIFAR-10: d = 2.41M, Shakespeare Corpus: d = 1.63M) 可以看出，OptEx 适用于大规模优化问题。其有效的并行更新机制使其在面对高维度的任务时依然能够保持良好的加速和收敛效果。

总结

总之，我们的OptEx框架在FOO领域代表了重要的进步。通过利用核化梯度估计实现近似并行迭代，OptEx有效地减少了收敛所需的顺序迭代次数，从而解决了FOO的传统效率问题。理论分析和广泛的实证研究验证了OptEx的可靠性和有效性，证实了其在各种应用中加速优化过程的潜力。

原文

OptEx: Expediting First-Order Optimization with Approximately Parallelized Iterations. Yao Shu, Jiongfeng Fang, Ying Tiffany He, Fei Richard Yu. In The 38th Conference on Neural Information Processing Systems (NeurIPS), 2024.

END

素材来源 丨光明实验室基础智能研究团队

编 辑 丨 李沛昱

审 核 丨 郭 锴